ĐÁNH GIÁ MÔ HÌNH NHÂN TỐ KHẲNG ĐỊNH

Đánh giá mô hình nhân tố khẳng định CFA bao gồm giá trị tin cậy, giá trị hội tụ, giá trị phân biệt, tính đơn hướng và giá trị liên hệ lý thuyết.

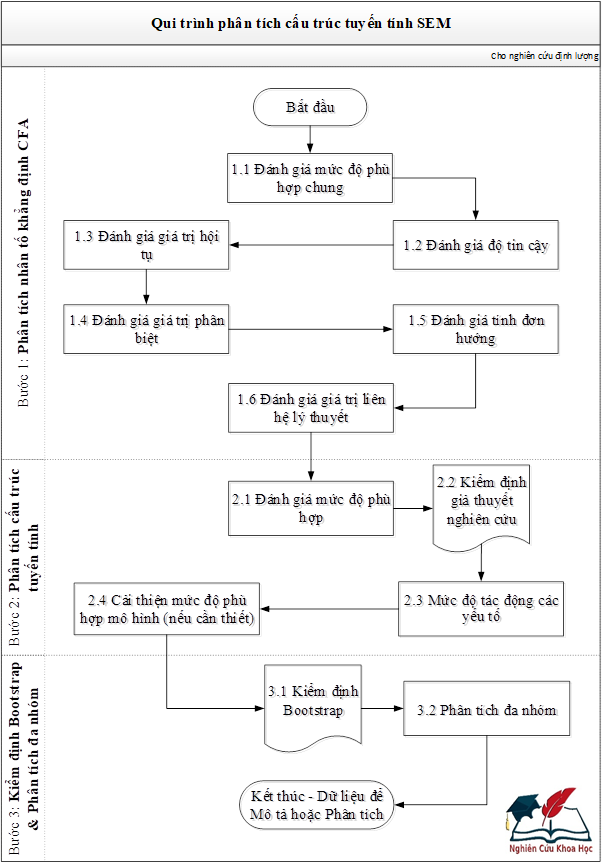
Qui trình phân tích Mô hình nhân tố khẳng định CFA và Mô hình cấu trúc tuyến tính SEM được thực hiện theo Hình 1.

[Nguồn: nghiencuukhoahoc.edu.vn, 2023]

Hình 1. Qui trình phân tích cấu trúc tuyến tính

Tham khảo thêm nội dung bài viết PHÂN TÍCH NHÂN TỐ KHẲNG ĐỊNH CFA và MÔ HÌNH CẤU TRÚC TUYẾN TÍNH SEM để nắm bắt các nội dung xây dựng mô hình.

1. Đánh giá độ tin cậy thang đo

Đánh giá độ tin cậy thang đo bằng độ tin cậy tổng hợp CR (Composite Reliability, ký hiệu: ρ_c) và hệ số tin cậy Cronbach’s Alpha.

Độ tin cậy tổng hợp CR được tính cho từng nhân tố đơn hướng, tương tự như cách áp dụng Cronbach's Alpha, sẽ chạy riêng cho từng nhân tố. Cronbach’s Alpha dùng để đo độ tin cậy của thang đo, nói lên tính nhất quán nội bộ của thang đo đó (Xem chi tiết thêm ở bài viết PHÂN TÍCH ĐỘ TIN CẬY THANG ĐO CRONBACH'S ALPHA. Công thức tính dựa trên sự tương quan lẫn nhau giữa các biến quan sát. Cronbach’s Alpha giả định rằng tất cả các biến quan sát đều có mức độ tin cậy như nhau, nghĩa là có khả năng tải vào nhân tố tiềm ẩn như nhau. Hơn nữa, Cronbach’s Alpha nhạy cảm với số lượng biến quan sát trong thang đo, và thường có xu hướng đánh giá thấp tính nhất quán nội tại. Do những hạn chế đó, độ tin cậy tổng hợp CR là một chỉ số đánh giá kĩ thuật phù hợp hơn để đo tính nhất quán nội tại. Phương pháp này hoàn toàn dựa vào hệ số hồi quy chuẩn hóa (Standardized Regression Weight).

Cronbach’s Alpha là một thước đo thận trọng về độ tin cậy (tức là, nó dẫn đến các giá trị độ tin cậy tương đối thấp). Ngược lại, độ tin cậy tổng hợp CR có xu hướng đánh giá cao hơn độ tin cậy nhất quán nội bộ, do đó dẫn đến ước tính độ tin cậy tương đối cao hơn. Vì vậy, nên xem xét và báo cáo cả hai tiêu chí. Khi phân tích và đánh giá độ tin cậy nội bộ của các thang đo, độ tin cậy thực sự thường nằm giữa hệ số Cronbach’s Alpha (đại diện cho giới hạn dưới) và độ tin cậy tổng hợp CR (đại diện cho giới hạn trên).

Theo Jöreskog (1971), độ tin cậy tổng hợp CR phải lớn hơn hoặc bằng 0,50, Bagozzi và Yi (1988) đề nghị trên ngưỡng 0,60 là “đáng mơ ước”. Trong khi Fornell và Larcker (1981) yêu cầu phải trên ngưỡng 0,70.

Công thức tính giá trị độ tin cậy tổng hợp:

trong đó,

ρ_c là độ tin cậy tổng hợp;

i là biến quan sát;

λ_i là hệ số hồi quy chuẩn hóa trong mô hình cấu trúc tuyến tính của biến quan sát thứ i;

1 - λ_i² là phương sai sai số đo lường của biến quan sát thứ i.

2. Đánh giá giá trị hội tụ

Giá trị hội tụ được đánh giá bằng hệ số tải nhân tố chuẩn hóa của CFA.

Theo Hair và cộng sự (2010), hệ số tải nhân tố chuẩn hóa của biến quan sát thỏa mãn ngưỡng về độ hội tụ là lớn hơn hoặc bằng 0,50, Anderson và Gerbring (1988) cho rằng thang đo đạt giá trị hội tụ khi các trọng số chuẩn hóa của thang đo đều lớn hơn 0,50 và có ý nghĩa thống kê (p-value < 0,05).

Phương sai trích trung bình AVE (Average Variance Extracted, ký hiệu: ρ_νc) hay trung bình phương sai trích được sử dụng để kiểm tra lại độ hội tụ bên trong của các biến quan sát trong cùng một khái niệm. Phương sai trích AVE được tính cho từng nhân tố đơn hướng. Theo Bagozzi và Yi (1988), trung bình phương sai trích AVE cần lớn hơn 0,50 để thỏa mãn giá trị hội tụ, Fornell và Larcker (1981) cho rằng phương sai trích phải lớn hơn hoặc bằng 0,50 là đạt yêu cầu, trong khi lớn hơn 0,70 được xem là tốt. Cũng giống như độ tin cậy tổng hợp, phương pháp này hoàn toàn dựa vào hệ số hồi quy chuẩn hóa (Standardized Regression Weight).

Công thức tính giá trị phương sai trích:

trong đó,

ρ_vc là trung bình phương sai trích;

i là biến quan sát;

λ_i là hệ số hồi quy chuẩn hóa trong mô hình cấu trúc tuyến tính của biến quan sát thứ i;

1 - λ_i² là phương sai sai số đo lường của biến quan sát thứ i.

Lưu ý:

Một cách nhanh chóng kiểm tra giá trị phương sai trích lớn hơn 0,50 mà không cần tính toán là kiểm tra trọng số hồi quy chuẩn hóa. Trọng số hồi qui chuẩn hóa cần lớn hơn 0,70 thì giá trị phương sai trích sẽ đảm bảo (giá trị xấp xĩ 0,70 cũng chưa chắc là một giải pháp tồi).

3. Đánh giá giá trị phân biệt

Theo Anderson và Gerbing (1988), hệ số tương quan giữa các khái niệm thành phần (yếu tố tiềm ẩn) phải nhỏ hơn 0,90 thì giá trị phân biệt đạt yêu cầu. Nhưng hệ số tương quan thường nhỏ hơn giá trị 0,90 rất nhiều.

Một cách cẩn thận hơn, giá trị phân biệt được đánh giá qua kiểm định hệ số tương quan tổng thể giữa các khái niệm có khác giá trị 1,00 không.

Qui trình kiểm định như sau.

(1) Giả thuyết

H₀: ρ = ρ₀ (bằng 1.0);

H₁: ρ ≠ ρ₀.

(2) Trị tới hạn

(3) Trị thống kê (t_α/2, n – 2), tra bảng Student.

(4) Kết luận: Nếu T > (t_α/2, n – 2), bác H₀.

Hoặc với sự hỗ trợ của phần mềm Excel, dùng hàm TINV để so sánh giá trị T và (t_α/2, n – 2). Hoặc dùng hàm TDIST(│CR│, n – 2, 2) để tính giá trị p-value cho kiểm định. Nếu p-value < 0.05 thì hệ số tương quan của từng cặp khái niệm khác biệt so với giá trị 1.0 (tức là ρ ≠ ρ₀) ở độ tin cậy 95%.

Bên cạnh đó, tiêu chuẩn Fornell-Lacker cũng được sử dụng rộng rãi để đánh giá giá trị phân biệt. Tiêu chuẩn này đòi hỏi rằng trung bình phương sai trích AVE của một khái niệm nên lớn hơn tương quan bình phương cao nhất của nó với khái niệm khác. Nghĩa là ρ_vc của một khái niệm phải lớn hơn tất cả hệ số r_i², trong đó r_i² là hệ số tương quan giữa khái niệm đó với những khái niệm khác.

4. Đánh giá tính đơn hướng

Theo Steenkamp và Van Trijip (1991), mô hình đo lường phù hợp với dữ liệu thị trường và không có tương quan giữa các sai số đo lường sẽ đạt được tính đơn hướng.

5. Đánh giá giá trị liên hệ lý thuyết

Các đánh giá từ một đến bốn được đánh giá thông qua mô hình đo lường, nghĩa là định lượng và có giới hạn rõ ràng. Riêng giá trị liên hệ lý thuyết được đánh giá trong mô hình lý thuyết (Anderson và Gerbing, 1988), nghĩa là mang tính định tính. Khi các đánh giá trên thỏa mãn thì mô hình đo lường tốt. Tuy nhiên, rất hiếm khi mô hình đo lường đạt được tất cả các vấn đề trên. Có trường hợp thang đo không đạt tính đơn hướng thì mô hình đo lường vẫn có thể được sử dụng để phân tích và diễn giải.

Ngoài ra, thống kê SMC (Square Multiple Correlation) cho mỗi khái niệm tiềm ẩn ngoại sinh (kết quả phân tích CFA của mô hình đo lường nêu trên), tương tự hệ số R² trong hồi qui tuyến tính, SMC là phương sai giải thích của mỗi khái niệm tiềm ẩn (Bollen, 1989).

Tài liệu tham khảo

1. Anderson, J. C., & Gerbing, D. W. (1988). Structural equation modeling in practice: A review and recommended two-step approach. Psychological Bulletin, 103(3), 411–423.
2. Bagozzi, R. & Yi, Y. (1988). On the Evaluation of Structural Equation Models. Journal of the Academy of Marketing Sciences, 16(), 74-94.
3. Bollen, K. A. (1989). A new incremental fit index for general structural equation models. Sociological Methods and Research, 17(), 303–316.
4. Fornell, C. & Larcker, D. F. (1981). Evaluating structural equation models with unobservable variables and measurement error. Journal of marketing research, (), 39-50.
5. Hair, J. F., Black, W. C., Babin, B. J. & Anderson, R. E. (2010). Multivariate Data Analysis. Publisher: Pearson; 7 Edition.
6. Jöreskog, K.G. (1971). Simultaneous factor analysis in several populations. Psychometrika, 36(), 409–426.
7. Steenkamp, J. B., & Van Trijp, H. C. M., (1991). The use of LISREL in validating marketing constructs. International Journal of reseach in Marketing, 8(40), 283-99.

 

Kết thúc.