Phương pháp sai lệch bình phương cực tiểu OLS

Phương pháp sai lệch bình phương cực tiểu OLS được vận dụng để giải quyết bài toán hồi quy với mong muốn cực tiểu sai lệch của phần dư.

1. Mô hình hồi quy đơn tổng quát

Có hai biến X và Y, trong đó Y phụ thuộc tuyến tính vào X. Với một giá trị X_i nào đó của biến X, giá trị tương ứng Y_i của biến Y được tính bằng công thức.

Y_i = β₀ + β₁X_i + ε_i

Trong đó,

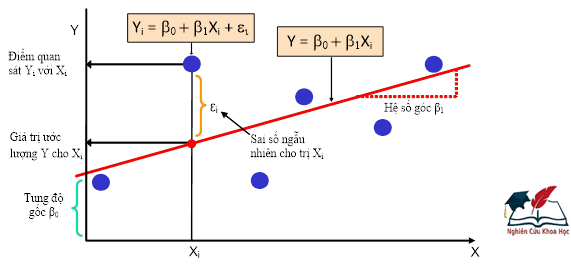
β₀: Tung độ gốc, là giao điểm của đường hồi quy với trục tung;

β₁: Hệ số góc, là độ dốc của đường hồi quy.

Hệ số β₀ thể hiện giá trị ước lượng của Y khi giá trị của biến X bằng không. β₁ thể hiện mức thay đổi của Y khi X thay đổi 1 đơn vị. ε_i là sai số phần dư biểu diễn ảnh hưởng của các yếu tố khác (các yếu tố không được nghiên cứu) đến Y. Một mô hình hồi quy có ý nghĩa thống kê khi ε_i biến thiên ngẫu nhiên, phân phối chuẩn với trung bình bằng không, phương sai không thay đổi theo các giá trị của X và độc lập tuyến tính (không tự tương quan với nhau). ε_i là sai lệch giữa giá trị ước lượng với giá trị thực.

Mô hình hồi quy tổng thể thể hiện mối liên hệ tuyến tính giữa X và Y được biểu diễn như sau.

Y = β₀ + β₁X + ε

Trong thực tế không thể định trị chính xác cho các tham số β₀, β₁ mà chỉ có thể ước lượng chúng từ dữ liệu của mẫu thu thập được. Mô hình hồi quy tuyến tính cho mẫu được biểu diễn như sau.

Y = b₀ + b₁X

Trong đó, b₀ và b₁: Hệ số hồi quy cho mẫu.

2. Phương pháp bình phương cực tiểu (OLS – Ordinary Least Squares)

Có các mẫu (Y₁, X₁), (Y₂, X₂), …, (Y_n, X_n) từ n quan sát. Tìm các giá trị b₀ và b₁ để ước lượng cho các tham số β₀ và β₁. Thường thì các điểm quan sát không nằm trên cùng một đường thẳng. Tuy nhiên, phương pháp bình phương cực tiểu sẽ vẽ đường thẳng đi giữa các điểm quan sát sao cho sai lệch phần dư ε_i là cực tiểu. Trong thực tế người ta sử dụng tham số sai lệch phần dư bình phương để tránh trường hợp tổng sai lệch phần dư bằng 0.

Cao độ của một quan sát: Y_i = b₀ + b₁X_i + ε_i (Hình 1).

[Nguồn: nghiencuukhoahoc.edu.vn, 2017]

Hình 1. Biểu đồ mô tả điểm quan sát Y_i, hàm hồi quy Y và sai lệch ε_i

Tức là: ε_i = Y_i - (b₀ + b₁X_i)

Tổng sai lệch phần dư bình phương:

Đạo hàm từng phần phương trình tổng sai lệch phần dư bình phương theo b₀ và b₁, sau đó gán biểu thức này bằng 0 được hệ 2 phương trình:

Giải hệ 2 phương trình nêu trên được công thức tính b₀ và b₁.

Hệ số góc b₁:

Tung độ gốc b₀:

Trong đó,

: Trung bình của biến độc lập;

: Trung bình của biến phụ thuộc.  

Kết thúc.

Để có thể thấy rõ cách thức vận dụng Phương pháp sai lệch bình phương cực tiểu OLS vào mô hình hồi quy, Chương 5 và Chương 6 của cuốn sách NGHIÊN CỨU KHOA HỌC TRONG KINH TẾ - XÃ HỘI & Hướng dẫn viết luận văn/luận án 2023 sẽ cung cấp cho bạn những ví dụ, dữ liệu, hình ảnh nghiên cứu thực tế. Tham khảo để thấy cách bạn sẽ được sở hữu một sản phẩm chất lượng thuộc Top 100 sản phẩm Phân tích kinh tế bán chạy của tháng tại Fahasa.com.

MUA SÁCH TẠI ĐÂY